definiția teoremei
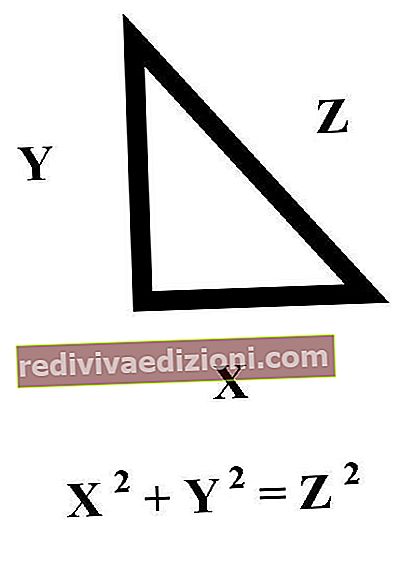Teoremele sunt necesitatea și preocuparea specială a matematicii și atunci când se vorbește despre acestea, se face referire la acele afirmații care pot fi dovedite adevărate într-un cadru logic .
În general, teoremele sunt compuse dintr-o serie de condiții care pot fi enumerate sau anticipate în avans la care se numesc răspunsuri . În urma acestora, va apărea concluzia sau afirmația matematică, care va fi evident întotdeauna adevărată în condițiile lucrării în cauză, adică, în primul rând în conținutul informativ al teoremei, ceea ce se va stabili este relația care există între ipoteza și teza sau finalizarea lucrării.
Dar există ceva inevitabil pentru matematică atunci când o anumită afirmație este plauzibilă pentru a deveni o teoremă și este că trebuie să fie suficient de interesantă în interiorul și pentru comunitatea matematică, altfel și din păcate, poate fi pur și simplu un deviz, un corolar sau pur și simplu o propoziție , nemaiputând deveni niciodată o teoremă.
Și pentru a clarifica problema un pic mai mult, este necesar, de asemenea, să distingem conceptele pe care le-am menționat mai sus, astfel încât, chiar dacă nu facem parte dintr-o comunitate matematică, putem recunoaște când este o teoremă, o lemă, un corolar sau o propunere.
O Lemă este o propunere, da, dar face parte dintr-o teoremă mai lungă. Corolarul, la rândul său, este o afirmație care urmează o teoremă și, în cele din urmă, propoziția este un rezultat care nu este asociat cu nicio teoremă anume.
La început am indicat că o teoremă este o afirmație care poate fi dovedită numai într-un cadru logic, în timp ce cu un cadru logic ne referim la un set de axiome sau sistem axiomatic și un proces de inferență care ne va permite să derivăm teoreme din axiomele și teoremele care au fost deja derivate anterior.
Pe de altă parte, secvența finită a formulelor logice bine formate va fi numită o dovadă a acestei teoreme.
Deși nu cu atenția specială pe care matematica o acordă teoremelor, discipline precum fizica sau economia produc de obicei afirmații care sunt deduse de la alții și care se mai numesc și teoreme.
